How often you pick up 15-17 HCP balanced hands
© boco_san, 2012/August
| Preface |
| Conclusion |
| Results Obtained |
| Appendix: How to Calculate the Probabilities |
| Appendix: When Has the Transition Occurred |
Preface
Once an opening 1NT bid used to mean balanced hands with (B) 16 -18 HCP . Meanwhile, perhaps in 1980's, the HCP range has changed to (A) 15 -17 HCP .
It is obvious that the choice (A) will bring more chance of 1NT opening, and will allow easier bidding sequence that will follow.
Surely often, but, how often ? Often to what extent ? In other words, how more often will you pick up 15 -17 balanced hands than 16 -18 ones ?
I know no answers in Bridge books nor in any WEB sites. So, I have tried for myself to evaluate probabilities of the (A) and (B) hands with balanced distributions, [4333], [4432], or [5332]. This distinction of balanced hands is so essential, because we never open 1NT on hands with a singleton or a void.
I'll start with the conclusion and then explain outline of the calculation. Details are given in the appendix below.
Conclusion
For the sake of hasty Bridge players, I will give first the conclusion.
When we compare the relative frequency of the two kind of hands,
(A) 15 -17 HCP balanced hands,
(B) 16 -18 HCP balanced hands,
the former will appear 1.371 times more frequently than the latter.
It is as well possible to do this comparison for
(a) 15 -17 HCP balanced as well as unbalanced hands,
(b) 16 -18 HCP balanced as well as unbalanced hands.
Although this comparison is totally meaningless, relative frequency of (a) to (b) turns out to be 1.387. This result is known in the WEB as 38%. So, I learned that the restriction to balanced hands was not important.
If you are interested in details, read more. Actually, it was a hard task for me.
Results Obtained
The problem here is to evaluate exactly the probabilities of picking up (A) 15 -17 and (B) 16 -18 HCP balanced hands.
When a player is dealt 13 cards, the number of card combinations amounts to 52C13 = 635,013,559,600 (about 635 billions). One can classify these deals according to HCP in the range 0 up to maximum 37. This doesn't solve our problem, however.
1NT opening requires balanced distributions in the four suits. Actually, only the three kinds of balanced distributions [4333], [4432] and [5332] will occupy 47.6% out of the 635 billion deals (which is somewhat astonishing in view of the possible 39 kinds of distributions). So, we encounter balanced hands almost once in two deals, which implies importance of how to bid on balanced hands (with only 3 kinds of distribution).
For the purpose mentioned above, we now classify the 635 billion deals according to both distributions and HCPs. The result is given in the following two big tables:
(1) Number of Hands
(2) Probability (in units of ‰ = 1/1000)
Click either table to see.
Both tables consist of 38 rows (for 0-37 HCP) × 39 columns (distributions) = 1,482 cells.
Table (1) gives the number of deals for specified HCPs AND distributions. They will sum up in total to 635 billion, as shown in the right bottom cell.
By simply dividing these numbers by 635 billion, we get the probabilities as shown in Table (2). Here, blanks mean that the corresponding probability is absolutely zero (and hence they never occur), while “0” means non-vanishing probability smaller than 0.001%. Because of the very small probabilities owing to the fine division into 1,482 cells, the probability values are shown in units of ‰ rather than %, and hence their total becomes 1000, again shown in the right bottom cell.
| HCP | [4333] | [4432] | [5332] | Total | % |
| 15 | 0.469 | 0.958 | 0.688 | 2.115 | (A) 15 -17 Total 4.866 |
| 16 | 0.355 | 0.723 | 0.182 | 1.596 | |
| 17 | 0.259 | 0.523 | 0.373 | 1.155 | (B) 16 -18 Total 3.550 |
| 18 | 0.180 | 0.363 | 0.256 | 0.799 |
This extracted table tells us that (A) and (B) will occur with absolute probabilities 4.87% and 3.55%, respectively, and hence we find the ratio of frequency 4.866 / 3.550 = 1.371.
To conclude, (A) will allow 37.1% more often 1NT opening than (B). Plainly speaking, while players (A) calls 4 times 1NT, players (B) will call only 3 times 1NT. This marked difference arises owing to the difference of probabilities of 15 and 18 HCP hands.
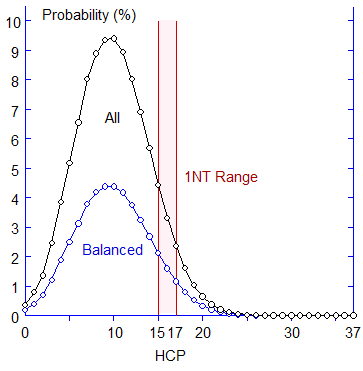 The situation may be understood clearly from the figure on the right.
The curves (circles) stand for probabilities against HCP taken in the
abscissa.
The situation may be understood clearly from the figure on the right.
The curves (circles) stand for probabilities against HCP taken in the
abscissa.
As mentioned above, the black circles (all hands, both balanced and unbalanced) show almost twice as large probabilities as the blue ones (balanced hands only). Both curves have a peak around HCP=10, since 40 HCPs are distributed among four players. Because the range 15 -18 is situated at the (right-hand) foot of this peak, the probability will increase considerably when one discards 18 HCP and takes 15 HCP.
Appendix: How to Evaluate the Probabilities
As mentioned above, we have 635 billion different ways in giving 13 cards to
a player out of 52 cards.
What we have to do here is to classify those 635 billion deals according to
combinations of HCP and distributions. Once such a classification is attained and the
number of deals belonging to them are obtained, the relevant probabilities are
readily obtained by simply dividing them with 635 billion.
As for the card distributions, we have [4333], [4432], … [13 000], which amount to 39 in total. We then multiply the multiplicity as given in the table on the right, which will take care for exchanging the cards among the 4 suits. The classification has to be done further on HCP.
Under a single constraint (either on the distribution, or HCP) the work goes simple. However, the simultaneous TWO constraints complicates the work. Frankly, I was quite at a loss for a long time how to attack the problem. I'll give below the answer which I have eventually found, but someone may find a cleverer solution.
OK, here we go.
As an example, let us take the distribution [4432], which occurs most frequently (21.6%). Then we have 4 spades, 4 hearts, 3 diamonds and 2 clubs. Similar distributions like [3424], etc. are covered by multiplying the multiplicity given above (6 in the present distribution).
For this distribution, let us enumerate the hands that have, say, 15 HCP.
Well, each suit will have one of the 16 honor holdings shown in the right table, where 4 down to 0 honors and corresponding HCPs are given in 16 ways. So, we give the honors to the four suits according to this table in turn.
The first possibility to consider with 15 HCP is
 AKQJ
AKQJ  AJxx
AJxx  xxx
xxx  xx,
xx,
where we gave AKQJ (10 HCP) to spades, AJ (5 HCP) to hearts. The other seven cards should be spot cards (2 to 10) with 0 HCP. While the honors have been specified uniquely, the spot cards have a lot of ways to be dealt. To be more specific, the spot cards are dealt in the following way:
The corresponding combination of ways in dealing is given by
Summing up these counts and multiplying with the above-mentioned
multiplicity 6, we obtain 2,976,568,236 for the
number of ways to deal 13 cards of [4333] distribution with 15 HCP.
The essence in the logic above is to multiply the combinations 9CN for the number N of spot cards to be dealt, which I didn't take notice for so long, because I have so much concentrated on honor cards.
The result has been verified by comparison of the totals for every columns and every rows, which may be evaluated the other way. As a matter of fact, the grand sum agrees with 635,013,559,600.
The HTML files for the above 2 tables (as well as the figure) were generated directly by means of the VB program to avoid errors in transcription.
I looked up some of my Bridge books and softwares to see when the transition from (B) to (A) has occurred, in particular, in USA:
| Distribution | Example | Multiplicity |
| All Different | [5431] | 4! = 24 |
| 2 equals | [4432] | 4! / 2! 2! = 6 |
| 3 equals | [4333] | 4 |
As for the card distributions, we have [4333], [4432], … [13 000], which amount to 39 in total. We then multiply the multiplicity as given in the table on the right, which will take care for exchanging the cards among the 4 suits. The classification has to be done further on HCP.
Under a single constraint (either on the distribution, or HCP) the work goes simple. However, the simultaneous TWO constraints complicates the work. Frankly, I was quite at a loss for a long time how to attack the problem. I'll give below the answer which I have eventually found, but someone may find a cleverer solution.
| Number of Honors | Honor Holding | HCP |
| 4 | AKQJ | 10 |
| 3 | AKQ | 9 |
| 3 | AKJ | 8 |
| 3 | AQJ | 7 |
| 3 | KQJ | 6 |
| 2 | AK | 7 |
| 2 | AQ | 6 |
| 2 | AJ | 5 |
| 2 | KQ | 5 |
| 2 | KJ | 4 |
| 2 | QJ | 3 |
| 1 | A | 4 |
| 1 | K | 3 |
| 1 | Q | 2 |
| 1 | J | 1 |
| 0 | none | 0 |
OK, here we go.
As an example, let us take the distribution [4432], which occurs most frequently (21.6%). Then we have 4 spades, 4 hearts, 3 diamonds and 2 clubs. Similar distributions like [3424], etc. are covered by multiplying the multiplicity given above (6 in the present distribution).
For this distribution, let us enumerate the hands that have, say, 15 HCP.
Well, each suit will have one of the 16 honor holdings shown in the right table, where 4 down to 0 honors and corresponding HCPs are given in 16 ways. So, we give the honors to the four suits according to this table in turn.
The first possibility to consider with 15 HCP is
 AKQJ
AKQJ  AJxx
AJxx  xxx
xxx  xx,
xx,
where we gave AKQJ (10 HCP) to spades, AJ (5 HCP) to hearts. The other seven cards should be spot cards (2 to 10) with 0 HCP. While the honors have been specified uniquely, the spot cards have a lot of ways to be dealt. To be more specific, the spot cards are dealt in the following way:
| 0 spade spot cards out of 9 spade spot cards, |
| 2 heart spot cards out of 9 heart spot cards, |
| 3 diamond spot cards out of 9 diamond spot cards, |
| 2 club spot cards out of 9 club spot cards. |
9C0 × 9C2 × 9C3 × 9C2
= 1 × 36 × 84 × 36 = 108,864.
Going this way, we will obtain
 AKQJ AKQJ
|  KQxx KQxx
|  xxx xxx
|  xx xx
| 9C0 × 9C2 × 9C3 × 9C2 | = 1 × 36 × 84 × 36 |
 AKQJ AKQJ
|  KJxx KJxx
|  Jxx Jxx
|  xx xx
| 9C0 × 9C2 × 9C2 × 9C2 | = 1 × 36 × 36 × 36 |
 AKQJ AKQJ
|  QJxx QJxx
|  Qxx Qxx
|  xx xx
| 9C0 × 9C2 × 9C2 × 9C2 | = 1 × 36 × 36 × 36 |
 AKQJ AKQJ
|  QJxx QJxx
|  Jxx Jxx
|  Jx Jx
| 9C0 × 9C2 × 9C2 × 9C1 | = 1 × 36 × 36 × 9 |
| etc. … |
The essence in the logic above is to multiply the combinations 9CN for the number N of spot cards to be dealt, which I didn't take notice for so long, because I have so much concentrated on honor cards.
The result has been verified by comparison of the totals for every columns and every rows, which may be evaluated the other way. As a matter of fact, the grand sum agrees with 635,013,559,600.
The HTML files for the above 2 tables (as well as the figure) were generated directly by means of the VB program to avoid errors in transcription.
When Has the Transition Occurred
I looked up some of my Bridge books and softwares to see when the transition from (B) to (A) has occurred, in particular, in USA:
- (A) Ned Dowley & Ellen Pomer: Standard Bidding with SAYC (2005).
- (A) Fred Gitelman: Learn to Play Bridge (2003).
- (A) Audrey Grant: ACBL Spade Series (2000).
- (A) Barbara Seagram & Marc Smith: 25 Bridge Conventions You Should Know, (1999).
- (A) William S. Root: The ABCs of Bridge (1998).
- (A) Mike Lawrence: Conventions (1996).
- (B) Audrey Grant: ACBL Club Series (1987).
- (A) William Root & Richard Pavlicek: Modern Bridge Conventions, (1981)
- (B) Charles H. Goren: Goren's New Bridge Complete, (1985)