


 Further Analysis of LoTT in Bridge
Further Analysis of LoTT in Bridge




[1] Object of This Work
[2] Reproducing Ginsberg's Work
[3] Separate Treatment
[4] Suit versus Suit
[5] Notrump versus Suit
[6] Independence of LoTT from HCP
We owe this history to three big names, Jean-René Vernes, Larry Cohen, and Matthew Ginsberg. Their contributions may be characterized by Discovery, Popularization, and Verification, respectively.
It was the genius of Vernes that invented a revolutionary concept «Total Tricks».
According to an interview held in Paris on 10, September, 2000, he answers, “J'ai decouvert la loi des levees totales vers 1955. J'ai commence a en parler, a partir de 1958, dans une serie d'articles, et je l'ai publiee sous sa forme actuelle en 1966 dans « Bridge Moderne de la Defense » (Editions du Bridgeur, 4e edition, juin 1987).”
Bridge is really a game where players compete in the difference in tricks they take, so it is difficult to imagine what significance the sum will have.
In his book, the above formula [2] for Notrump was given in a table of 3×4 = 12 cells, which makes the Law formula seem somewhat complex, but never confusing.
In expectation of how Vernes himself theoretically accounts for his Laws above, I purchased his book for € 31.37. The result was totally against my expectation.
His study was not theoretical. He gathered and studied world-championship deals over 10 years, and discovered that the Law holds statistically.
If we are to do such a study today, we could use personal computers and collect lots of information through Internet. In 1950's, no personal computers were available, nor even pocket calculators. But it appears that he was quite determined. He writes in his preface (my translation).
Vernes's book written in French remained unnoticed for a long time, perhaps because it was not in English. Almost 30 years later, LoTT has got all of a sudden popularized in the hands of Larry Cohen.
His arguments based on the Chart logic was very convincing to explain the relationship between the Law and the Rule. As to this relation between them, Vernes gave no good explanations. He simply proposed a practical Rule and gave no theoretical support to it based on the Law. Cohen clearly showed that the Chart logic bridges a gap between them.
In good applications, separate understanding of
Law(LoTT), Rule (for the Safe Level), and Chart logic
is necessary. For example, LoTT is independent of HCP, vulnerabilities, and scoring system (IMPs or MatchPoints), whereas the Rule and the Chart depend on them.
In the computer age, rather than studying the live hands actually played (as Vernes did), Ginsberg tried on statistical verification of the Law on a large number of random deals generated on a computer.
In this respect, he was in a singular position since he had developed a double-dummy solver for the purpose of using it in his software GIB (Ginsberg Intelligent Bridge Player)
He has put 446,841 random deals into his solver, and found that the result closely verifies the Law formula [1] for the Suit-Suit case.
His report gives only numerical result in two tables, from which I have constructed a figure (click) like this. Here, the ordinate and abscissa correspond to the left and right-hand sides of eq [1]. The blue straight line with inclination 45°represents eq [1], while the red crosses × stand for the average Total Tricks available for give Total Length.
Concurrently with his work, he generously released a library of 717,102 random deals (together with results of double-dummy analysis) and left it in his FTP site, which is now unfortunately closed because of spin off.
[1]. Object of This Work
So far, so good for the first law (for suit contracts).
Now, the second law (for Notrumps) remains to be studied in the same way.
For this purpose, I have developed two softwares ViewDDLlib and LottAnalyzer,
which are now open for public use.
But, wait for a moment ! My software should work as nicely as Ginsberg's does, when his setting (or, description)
is followed. It must reproduce previous results for it to be called scientific.
So, I aim:
(A) To reproduce Ginsberg's result according to his description,
(B) To work out statistics, with Notrump and Suit deals treated separately.
[2]. Reproducing Ginsberg's Work
In this section, I will try to reproduce the result of Ginsberg, as far as possible.
Although the simple description of Ginsberg contains some uncertainties (or artifacts),
I chose the options called "Ginsberg" and "Length" in my
LottAnalyzer.
Here, all the 717,102 deals are played in suit contracts.
Notrump calls are forbidden at all. As a result, for example, balanced hands with 3NT are forced to bid
some suits, which cannot possibly attain a game.
Trump suits are selected solely by Length.
Score nor priority of contracts are never considered.
For example, when 4 and 4
and 4 are both makeable, Clubs are automatically selected if longer than Spades. Furthermore, Clubs will remain as such
and will have to concede to opponents, if they compete with 4
are both makeable, Clubs are automatically selected if longer than Spades. Furthermore, Clubs will remain as such
and will have to concede to opponents, if they compete with 4 or 4
or 4 ,
even though we can make 4
,
even though we can make 4 with shorter Spades as the trump suit.
with shorter Spades as the trump suit.
Artificial declarers, although quite dubious, possessing fewer trumps than partner, are allowed to declare in this
virtual Bridge (#1485).
The result is shown below in a table and compared with Ginsberg's,
| Reproducibility check of LottAnalyzer for Ginsberg's result | |||||||
| Ginsberg (total.ps.gz), | LottAnalyzer ( Ginsberg + Length Option) | ||||||
| Total Length | number of samples | average of deviation | average error | Total Length | number of samples | average of deviation | average error |
| 14 | 46,944 | −0.15 | 0.63 | 14 | 75,608 | −0.15 | 0.63 |
| 15 | 47,281 | −0.14 | 0.64 | 15 | 75,592 | −0.14 | 0.64 |
| 16 | 120,525 | 0.10 | 0.70 | 16 | 193,690 | 0.10 | 0.70 |
| 17 | 102,184 | 0.02 | 0.75 | 17 | 163,632 | 0.02 | 0.75 |
| 18 | 69,792 | −0.01 | 0.83 | 18 | 111,997 | −0.01 | 0.83 |
| 19 | 37,561 | −0.22 | 0.87 | 19 | 60,416 | −0.21 | 0.86 |
| 20 | 15,845 | −0.50 | 0.99 | 20 | 25,545 | −0.50 | 1.00 |
| 21 | 5,041 | −0.89 | 1.20 | 21 | 8,123 | −0.89 | 1.20 |
| 22 | 1,286 | −1.31 | 1.48 | 22 | 2,035 | −1.28 | 1.46 |
| 23 | 237 | −1.78 | 1.83 | 23 | 396 | −1.83 | 1.87 |
| 24 | 45 | −2.22 | 2.27 | 24 | 68 | −2.22 | 2.25 |
| Total | 446,741 | −0.05 | 0.75 | Total | 717,102 | −0.05 | 0.75 |
This good agreement means the following two:
(1) My LottAnalyzer is running nicely (at least in the Ginsberg setting), and perhaps the data handling is right (in particular, correctly reading his double-dummy library file).
(2) It has now become apparent that Ginsberg did not pay due attention to trump suits, because neither did I in the above analysis (right). He simply chose longest suits as trumps and paid no attention to score nor to Notrump play.
Having established this, we go on to the next step.
I am yet wondering about the difference in the sample size, 446741 and 717102. Didn't he use this library in his analysis ?
[3]. Separate Treatment
We now take the statistics, after dividing the deals into two categories, Suit and Notrump.
Here, Notrump hands are required to take 7 tricks or more in Notrump and less score in
suits. Otherwise, deals are classified into the former.
As a natural consequence, 4 and 4
and 4 are preferred to 3NT, while
3NT is preferred to 5
are preferred to 3NT, while
3NT is preferred to 5 and 5
and 5 .
.
As a result, 717102 deals in total are divided into 501591(suits) and 215511(NT).
Several artifacts mentioned above in [2] are now removed.
They are mostly overcome by considering Score rather than Length in
determining the strain. Surely, longer suits do not necessarily bring better score,
as obvious from the above mentioned example of 4 and 4
and 4 .
.
Once competition takes place, however, (i.e., when our high-score contract is
overwhelmed by their contract), other strains with more tricks (but lower score) are pursued.
Say, we have 3 and 4
and 4 , both makeable.
We will remain in 3
, both makeable.
We will remain in 3 so long as competition does not take place.
But if opponents are able to bid 4
so long as competition does not take place.
But if opponents are able to bid 4 , we change our denomination to 4
, we change our denomination to 4 .
This is an example where competition changes trump suits.
.
This is an example where competition changes trump suits.
In addition, artificial declarers are forbidden, by requiring them to have
(more HCP, when equal in length),
more HCP than partner in Notrump.
[4]. Suit versus Suit
Although I tried best improvements (so I think) on Ginsberg's work,
the result turned out to be similar to his.
Comparison will be made now in the format below:
Here, deviation will mean
| Comparison between Ginsberg and LottAnalyzer for Suit Contracts | ||
| Ginsberg (total.ps.gz) | LottAnalyzer (Standard+Score Option) | |
| +1 trick deviation | 22.4% | 31.6% |
| 0 trick deviation | 40.0% | 38.8% |
| −1 trick deviation | 24.5% | 14.9% |
| Average Deviation(tricks) | −0.05 | +0.37 |
| Average Error(tricks) | 0.75 | 0.79 |
| Sample Size | 446,741 | 389,908 |
For example, "+1 trick" means that LoTT underestimates Total Tricks by one trick.
"Average deviation" means its average over the entire deals.
"Average error" stands for average of its absolute magnitude (|deviation|).
It is different from the standard deviation commonly used in statistics, but we follow here the convention started by Jean-René Vernes.
From this table, we observe that both yield an almost equal value for the average error, 0.75 and 0.79 tricks, respectively. So, an error of 0.8 tricks is the best value known from the double-dummy analysis.
As a matter of fact, I have started this work in the hope of reducing the average error (or rather, variation), by proper selection of trump suits. Notrump hands have been excluded in LottAnalyzer, while Ginsberg includes them as suit contracts. Nevertheless, my efforts did not reduce the average error.
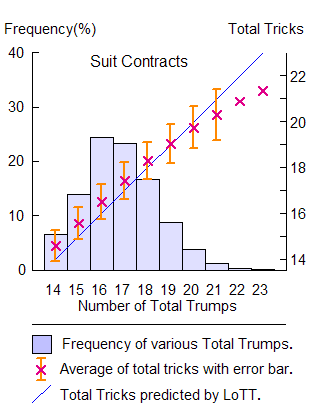
So far for error. As for the magnitude of deviations, LottAnalyzer tells us that the LoTT underestimates Total Tricks by 0.37 tricks on the average. This is most clearly seen in the figure output from LottAnalyzer (on the left). In most frequent cases of 15-18 total trumps, the LoTT almost constantly underestimates by 0.4 tricks, and will tend to overestimate with increase in total trumps (for more details, ask LottAnalyzer).
Overall behavior is quite similar to the one you have already seen above (to appear now in a separate window), except a vertical constant 0.4 tricks. Just view them in parallel and compare.
So, what to conclude ?
Ginsberg's work revealed that if you choose longest suits as trumps, you can most profitably expect the LoTT to hold on the average.
In bridge table, however, trump suits are determined through more deliberate considerations. Length is certainly important, but it cannot be all.
My best treatment of trump selection together with exclusion of Notrump hands in LottAnalyzer tells us that LoTT will underestimate total tricks by 0.37 tricks.
You might say, "Oh, that is too simple. I am already doing positive adjustments with a long side suit".
You are indeed right in doing so,
You have to remember here that Ginsberg's analysis and mine are statistical by nature. The conclusions drawn from them are almost exact because of the huge sample size, but they can tell us nothing for each deal. You have to do right judgments for each deal at Bridge table.
Ginsberg's result shows that if you take the longest suit (instead of the trump length) in the LoTT formula, you will need no more corrections on 40% deals. Further corrections are necessary on 60% deals. Since the frequencies of positive and negative corrections are nearly equal, they cancel out on the average and makes it more appealing.
As for the conventional LoTT formula, the LottAnalyzer tells us that we need no corrections on 39% deals. The positive average deviation 0.37 tricks will mean that one has to do positive corrections more often than negative ones. You will pick up hands which need +1 correction twice more often than those which need −1 correction.
These are the conclusions we learn from the statistical LoTT analysis.
[5]. Notrump versus Suit
Now, we proceed to deals where one side is going to play Notrump.
Here arises a problem as to which formula to take as the LoTT for Notrump.
Most popular version is the one due to Larry Cohen (in To Bid or
Not To Bid), which reads,
Earlier, however, Jean-René Vernes had proposed his own formula:
Here, I would confuse to add one more (and call it Modified Vernes)
| Results of | |||
| Law Formula | Cohen | Vernes | Modified Vernes |
| +2 trick deviation | 13.5% | 21.5% | 5.0% |
| +1 trick deviation | 32.5% | 40.8% | 21.5% |
| 0 trick deviation | 37.3% | 25.4% | 40.8% |
| −1 trick deviation | 11.4% | 5.9% | 25.4% |
| Average Deviation | 0.62 tricks | 0.95 tricks | 0.05 tricks |
| Average Error | 0.87 tricks | 1.09 tricks | 0.73 tricks |
| Sample Size | 145,140 | 145,140 | 145,140 |
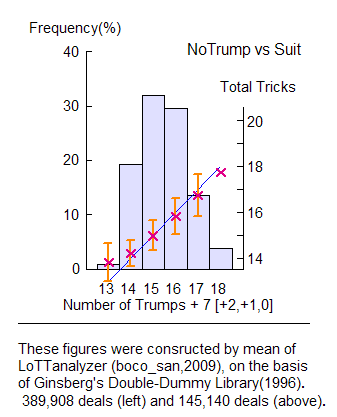 I added a row for the +2 deviation, since it occurs so often in Cohen and Vernes.
If you are to choose one among the three according to a good sense in statistics,
Modified Vernes is best, not because
it best accords with the law (with the 0.05 average),
but because it has least average error (or least variations).
I added a row for the +2 deviation, since it occurs so often in Cohen and Vernes.
If you are to choose one among the three according to a good sense in statistics,
Modified Vernes is best, not because
it best accords with the law (with the 0.05 average),
but because it has least average error (or least variations).
The graph on the right plots the result for this case. You see the crosses in wine color nicely sit on the blue line predicted by the proposed law formula. So, it is the best among the three.
However, to a great regret of Vernes, his correction has turned out to be worst. It was perhaps unavoidable since only 73 deals were available to him (which were played on two tables, one in NT and the other in a suit, and the suit had to be common).
We have found that the Modified Vernes formula is most reliable in Notrumps, with an average error (0.73 tricks) comparable to that in suits (0.79 tricks). It works better than the Cohen formula.
Nevertheless, I will recommend here Cohen's law formula, which is simple and easy to keep in memory. You have only to learn the magic number 7 by heart, and consider corrections according to your hand and the bidding sequence. You will sometimes try a correction of TWO tricks with a void, remembering the Modified Vernes law formula.
[6]. Independence of LoTT from HCP
This note is for someone who believes that the LoTT holds only in a limited range of HCP, or believes that Vernes so said.
In truth, Jean-René Vernes admits three kinds of corrections in the LoTT. However, he speaks nothing on HCP concerning LoTT. It is only when he comments on his Rule (la Règle de Sept à Douze, the Rule for the Safe Level) [French original, English version] that he mentions something on HCP.
So, the requirement for HCP is NOT for his LAW, BUT for his RULE. Remember that Vernes was careful in his writing.
| Result of
under the Four Different Requirements for HCP | ||||
| 0-40 | 15-25 | 17-23 | 0-14, 26-40 | |
| +2 trick deviation | 9.7% | 9.5% | 9.3% | 10.2% |
| +1 trick deviation | 31.5% | 31.5% | 31.5% | 31.0% |
| 0 trick deviation | 38.4% | 38.8% | 39.2% | 37.0% |
| −1 trick deviation | 15.2% | 14.9% | 14.9% | 16.0% |
| Average Deviation | 0.36 tricks | 0.37 tricks | 0.36 tricks | 0.34 tricks |
| Average Error | 0.79 tricks | 0.79 tricks | 0.78 tricks | 0.82 tricks |
| Sample Size | 506,581 | 389,908 | 280,383 | 116,673 |
Download from my site below and use. You will find more tables and graphs.