Adjusting the Law of Total Tricks
Since the Law of Total Tricks will come up with the right answer at best 40% of the time, any player who wants to use it simply has to adjust the formula. On this page, we will take a closer look at what Jean-René Vernes and Larry Cohen have written on the subject.
What Vernes said
When Jean-René Vernes published his article in The Bridge World, June 1969, he mentioned a few factors which he deemed important. This is what he wrote:
- The existence of a double fit, each side having 8 cards or more
in two suits. When this happens, the number of total tricks is frequently
one trick greater than the general formula would indicate. This is the most
important of the "extra factors".
- The possession of trump honors. The number of total tricks is often
greater than predicted when each side has all the honors in its own trump
suit. Likewise, the number is often lower than predicted when these honors
are owned by the opponents. (It is the middle honors — King, Queen, Jack —
that are of greatest importance.) Still, the effect of this factor is
considerably less than one might suppose. So it does not seem necessary to
have a formal "correction" but merely to bear it in mind in close cases.
- The distribution of the remaining (non-trump) suits.
Up to now we have considered only how the cards are divided between the two sides, not how the cards of one suit are divided between two partners. This distribution has a small, but not completely neglible, effect.
Double fit
Let's see if Vernes was right regarding these corrections.
If we start with his first factor, the double fit, we agree with him.
But have you ever wondered
why there should be extra tricks. In his excellent book Matchpoints
(Devyn Press, 1982), Kit Woolsey writes (on p. 170) "... the second suit is
sort of another trump suit, so both you and your opponents may take more tricks
than the law of total tricks would predict even on relatively balanced hands."
Thinking of the second fit as "another trump suit" is a wide spread belief. But it happens to be wrong. Actually, there is nothing good for your side to have two suits of 8 or more cards — but it is good for your side when the opponents have it...
Let's use Woolsey's example from p. 171 to show what we mean:
|
|
In the left diagram, both sides can take 9 tricks with 8 trumps, so this is a "+2" deal.
Now we move ♣3 from East to South and, in return,
♦6 from South to East (right diagram):
The deal is no longer a double fit, but North-South still take 9 tricks.
East-West, on the other hand, take only 8.
Why ?
The answer is simple. It has to do with the distribution. In both these deals, North-South's SST [Short Suit Total] is 4, and they have the same number of Working Points. Whether South has 4 diamonds and 3 clubs, or the opposite, it doesn't matter to his side. For East-West, however, East's getting ♦ instead of ♣ meant their SST went up from 4 to 5, which is equivalent to getting a loser.
 | A K 5 4 | |
 | 5 3 2 | |
 | A Q 8 2 | |
 | 10 6 | |
 10 7 6 10 7 6
| 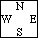
|  9 2 9 2
|
 A 7 4 A 7 4
|  K Q J 10 6 K Q J 10 6
| |
 9 6 4 3 9 6 4 3
|  10 5 10 5
| |
 K J 8 K J 8
|  A Q 5 3 A Q 5 3
| |
 | Q J 8 3 | |
 | 9 8 | |
 | K J 7 | |
 | 9 7 4 2 |
Had South swapped his ♦6 with West' ♣4 instead, nothing would have happened:
No double fit any longer, but the same number of tricks as in the original
deal.
Since the swap changed the SST of neither side, we shouldn't be
surprised that the total trick count doesn't change. It is still a "+2" deal.
The reason why there often are extra tricks when both sides have two suits of
8+ cards has to do with the distribution,
nothing else. And you will find the answer in your short
suits.
When opponents have two suits of 8+ cards,
your SST will never be greater than 4 —
and when they have a suit of 8+ length with a
second longest suit of 7 cards (or shorter),
then your SST can be 5.
 | K 8 7 6 | |
 | K J 8 3 | |
 | 8 7 6 | |
 | J 2 | |
 9 2 9 2
| 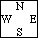
|  10 3 10 3
|
 A 7 4 A 7 4
|  10 9 2 10 9 2
| |
 K Q 9 3 K Q 9 3
|  J 10 5 4 J 10 5 4
| |
 K 10 9 3 K 10 9 3
|  A Q 8 6 A Q 8 6
| |
 | A Q J 5 4 | |
 | Q 6 5 | |
 | A 2 | |
 | 7 5 4 |
If you ever thought it was good to have two suits of 8+ cards, this example shows that you were wrong. Here, the two sides are equally strong, but North-South take 9 tricks, while East-West take 8. Why ?
The fact that North-South have 9 trumps and East-West 8 has nothing to do with it. If you think so, move a heart from North to East and move a club back. Then, both sides take only 8 tricks, but the total trump count is still 17.
Since both sides have their share of the deck (North-South have 20 WP [Working Points]; East-West have 19 WP), how many tricks they take is reflected in their SST [Short Suit Total]. And since North-South have 4, East-West 5, it is easy to understand why North-South take one more trick than their opponents in the diagram above.
So, when a deal has a double fit, i.e., when both sides have two suits of 8+ cards, an extra trick doesn't come from your second 8-card suit, but from the fact that your SST is guaranteed to be 4 or less. The gain comes from opponents' second 8-card suit, never from yours.
 | 10 9 8 | |
 | K Q 10 4 | |
 | A 3 | |
 | Q 9 8 7 | |
 Q J 7 6 Q J 7 6
| 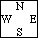
|  A K 4 3 A K 4 3
|
 9 3 2 9 3 2
|  A 5 A 5
| |
 Q 10 9 2 Q 10 9 2
|  J 7 6 5 J 7 6 5
| |
 3 2 3 2
|  A 6 5 A 6 5
| |
 | 5 2 | |
 | J 8 7 6 | |
 | K 8 4 | |
 | K J 10 4 |
If we swap one of the spot cards in East's diamonds with another in a side-suit (thus giving up the second 8-card suit), they will still try an adverse ruff, and will succeed if their diamonds are 4-2 and will lose if 3-3.
And we aren't better off playing in a diamond partial, since then North-South can arrange a ruff in spades. Having two 8-cards was no good for East-West.
The same can be said for North-South. They too will suffer an adverse ruff, no matter which suit (♥, ♣) they choose as the trump. But had they had 7 cards in their second longest suit, they would have gained one trick, if opponents have the 3-3 break in that suit.
Now you will probably wonder "If both sides have half the deck in working points (North-South have 19 WP, East-West have 21 WP) and each side has an SST of 4, why do they take only 8 tricks ? What's wrong with your formula ?"
There's nothing wrong with it. The formula predicts how many tricks you can
take if nothing bad happens. When there occurs an adverse ruff, something bad does
happen, and no matter which method of valuation you use, you can't predict it.
Another way of looking it is this: When there occurs an adverse ruff
with an otherwise useless trump, what happens is that your side loses some of
its WP.
When East-West play a contract in ♠, and North-South take a ruff in ♦,
its effect will be as if East-West had zero WP in ♦. The
first, second and third diamond rounds were all won by North-South. So the
ruff has reduced East-West's WP down to 18 and an SST of 4, equalling 8
tricks.
And the same goes for North-South as well: if East-West arranges an adverse ruff,
North-South haven't 6 WP in their second longest side-suit, only 3 WP. The fact
that both sides win a trick with a fourth-round winner isn't reflected in their
WP; it's a part of the distribution.
Trump honors
What about Vernes' second factor, possession of trump honors ? Would you belive us, if we told you this factor is unnecessary , and looking at WP and SST is much better ? OK, here we go.
| West | East | |
 K Q K Q
|  J 4 J 4
|
North-South's trump suit is hearts. If East-West's hearts are 2-2, as here,
both sides will lose one heart trick, if they declare the hand.
| West | East | |
 K Q 4 K Q 4
|  J J
|
Assuming their second shortest suit is of length 3, their SST in the first case is 5, in the second case 4. But they don't take more tricks because what they gain in distribution in the second case (going from 5 to 4 in SST) is balanced by a loss in WP (going from 3 WP in the first case to 0 WP in the second). Since 3 WP represent one trick, the loss in WP is compensated by the gain in distribution.
For North-South the difference between 3-1 and 2-2 is one trick. And that is reflected in their WP. When trumps break evenly, they have the equivalent of 6 WP in trumps (losing one trump trick only), but if trumps are 3-1, they only have 4 WP in trumps (losing two trump tricks).
If North-South have all trump honors instead, the difference between 2-2 and 3-1 is worth a trick to the East-West side, because , when East-West declare, North-South's 10 HCP in hearts only take one trick on defense instead of two. Here, the gain is purely distributional. The extra trick doesn't come from one side's having all trump honors, it comes from a reduction of losers in the opponents' strong suit.
There's nothing bad in having all trump honors, of course, but no extra tricks pop up from that. If there are more tricks than trumps on a deal where one side or both have all trump honors, then it's a result of the distribution.
Distribution of a suit between the partners
What shall we say about Vernes' third and final correction, that the distribution in a suit between two partners "has a small, but not completely neglible, effect" ? To put it mildly, we think this is a serious understatement.
Sometimes, a gain in distribution for one side is a gain both on defense and
on offense.
But often the gain is either only on defense (e.g., when you had ♣KQx
opposite a singleton ♣J, instead of a ♣KQ doubleton opposite ♣Jx) or only on offense (e.g., when
you had ♣xxx opposite a singleton ♣x, instead of ♣xx opposite a doubleton ♣xx).
Are these situations really rare ?
Of course not.
If a gain in distribution is a loss in WP, nothing happens. Suppose you have a side-suit like ♣AKx opposite ♣Qxx and an SST of 5. If we change that suit to ♣AKxx opposite ♣Qx (and keep everything else as it is), your SST goes down to 4, but if you can't use the suit for pitch, the gain in distribution is balanced by a loss in WP (going from 9 WP in this suit down to 7 WP). Then, nothing happens. This is not unusual, but it is definitely not the norm, as Vernes seems to think.
 | A J 8 7 | |
 | A K 4 3 | |
 | 5 4 3 | |
 | J 8 | |
 9 6 9 6
| 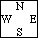
|  5 2 5 2
|
 J 9 2 J 9 2
|  10 7 6 5 10 7 6 5
| |
 A K 9 6 A K 9 6
|  J 10 2 J 10 2
| |
 9 7 6 2 9 7 6 2
|  A 10 5 3 A 10 5 3
| |
 | K Q 10 4 3 | |
 | Q 8 | |
 | Q 8 7 | |
 | K Q 4 |
27 HCP, 9 strong spades, and two doubletons, but since the defenders can win the first four tricks, there is no game. When that happens, North-South may realize that they have only 20 WP (♥Q, ♦Q and ♣QJ don't take tricks; therefore, they are not working). Add that to their SST of 4, and you understand why these cards aren't good enough for game against best defense.
Another case where a change in the side-suit distribution will result in a change in the total tricks is when adverse ruffs take place. Total tricks then go down.
 | A J 8 7 | |
 | K J 10 2 | |
 | 5 4 3 | |
 | 8 7 | |
 9 9
| 
|  6 5 2 6 5 2
|
 6 5 6 5
|  A 9 4 3 A 9 4 3
| |
 Q 10 8 2 Q 10 8 2
|  J 9 6 J 9 6
| |
 Q 10 9 6 5 2 Q 10 9 6 5 2
|  A J 3 A J 3
| |
 | K Q 10 4 3 | |
 | Q 8 7 | |
 | A K 7 | |
 | K 4 |
North-South take 11 tricks in spades. They have 1 HCP less than in the
previous example, and still an SST of 5, but since declarer has time to pitch
his ♦ loser under dummy's fourth heart, the fourth heart
is worthy of 3 WP. Therefore, the North-South hands are counted to have 29 WP.
Note that if South's ♦K
had been the ♣A instead (and the distribution the same), North-South gains
1 HCP, but loses 2 WP (and a trick): Then, after ♦ lead, dummy's fourth
heart is worth nothing.
On the other hand, East-West take 8 tricks, which may be expected from 14 WP and 3 SST. If we swap ♠6 and ♥5 between the East and West hands, we keep their SST at 3 (and their tricks at 8), but that swap will remove 2 tricks from North-South.
 | A J 8 7 | |
 | K J 10 2 | |
 | 5 4 3 | |
 | 8 7 | |
 9 6 9 6
| 
|  5 2 5 2
|
 6 6
|  A 9 5 4 3 A 9 5 4 3
| |
 Q 10 8 2 Q 10 8 2
|  J 9 6 J 9 6
| |
 Q 10 9 6 5 2 Q 10 9 6 5 2
|  A J 3 A J 3
| |
 | K Q 10 4 3 | |
 | Q 8 7 | |
 | A K 7 | |
 | K 4 |
East-West take the same 8 tricks if they declare, but North-South suffer two heart ruffs and take only 9 tricks.
What has happened is that North-South no longer have 9 WP in hearts as before. Two winners were ruffed away, so North-South lose 6 WP. Since 6 WP is equivalent to 2 tricks, we know why North-South take two tricks less in this scenario. The fourth heart is still useful for a discard, which means they have 3 WP in the suit.
What Cohen said
Larry Cohen also talks about corrections in his books, but he uses the term adjustments instead, and since these books have made a big impact on the bridgeplaying community of today we will stick with his term.
He divides the adjustment factors into two groups: Negative (suggest total tricks will be less than total trumps) and Positive (suggest total tricks will be greater than total tricks). The factors are:
- Purity
- Fit
- Shape
Purity
Negative Purity is defined as "minor honors in opponents' suits and/or poor intermediates in your own suits", while Positive Purity is "No minor honors in opponents' suits and/or good intermediates in your own suits". What he means is that if one side, say North-South, has a slow loser in one of their long suits if they play the hand, that trick often is worth nothing for East-West when they declare.
 | K 10 8 3 | |
 | K 6 5 4 | |
 | A 7 6 | |
 | 9 8 | |
 Q 5 4 Q 5 4
| 
|  J 2 J 2
|
 A 9 2 A 9 2
|  8 7 3 8 7 3
| |
 K Q J 9 K Q J 9
|  10 8 5 10 8 5
| |
 Q 3 2 Q 3 2
|  A J 10 7
6 A J 10 7
6
| |
 | A 9 7 6 | |
 | Q J 10 | |
 | 4 3 2 | |
 | K 5 4 |
In this example, East-West's spade combination is worth one trick on defense, but it is worthless if they declare and play in ♣ (when a spade is led, the defenders N-S can shift to hearts to stop declarer from establishing ♠Q for a useful discard).
Which side gains ?
One problem with looking at all tricks together, as the Law of Total Tricks does (instead of taking one side at a time), is that it doesn't say which side is affected. In this example, East-West has a slow trump trick on defense, so it is natural to think that the loss is for North-South. But it isn't. It is easy to understand if you do as we teach and view the deal in terms of WP and SST.
North-South have 20 HCP, and all of them are working. Their SST is 5. If we put them together, the formula says "8 tricks." And the formula is right, again.
East-West also have 20 HCP, but since their spade honors are useless if they declare, they have only 17 WP. Since they too have an SST of 5, we can figure out that they should take 7 tricks. And they do, in fact.
Now suppose your side has 4 cards in their trump suit, Q, J, 10 and 2. A first effect will be that your 3 HCPs are not working for you. A second effect is that your distribution will tell you how many WP the opponents have in that suit. In case your cards are split 2-2, their 9 trumps headed by AK is worth 10 WP (no losers), which means that they will take one more trick than in the 3-1 case (and you will take a trump trick on defense).
What about your side ? Gain one, you say ? Maybe. The difference between 2-2
and 3-1 is worth one trick, if and only if your SST is reduced by one. Suppose
your suit is ♠ and their suit is ♣.
If you have 5-4 in the majors and
your partner have a flat hand, it doesn't matter if you are 2-2 or 3-1 in the minors;
in both cases your SST will be 4. So, if you go from 2-2 to 3-1 in the
opponents' suit (by trading a club for a diamond with your partner), that change
isn't worth a trick if you at the same time go up from 2 to 3 in another suit.
By looking at the two shortest suits, as we do, we avoid mistakes like
thinking "one less loser in their suit = one more trick to us". Since each hand
consists of 13 cards, it all depends on which card you got instead. If a gain in
one suit is compensated by a loss in another, nothing happens.
To summarize: If your cards in their suit are 2-2, the opponents gain a trick on offense, since they gain 3 WP. If your cards in their suit are 3-1, you gain a trick if your SST goes down by one. In the first case, the gain came from extra WP, in the second it came from improved distribution.
Why "purity" doesn't explain anything
In To Bid or Not to Bid, Larry Cohen wants us to look at a "totally pure deal" (page 225):
 | A K 10 9 3 | |
 | 8 5 | |
 | A 2 | |
 | 8 7 6 5 | |
 8 7 8 7
| 
|  2 2
|
 7 4 7 4
|  K 10 9 6 3 K 10 9 6 3
| |
 J 10 8 5 4 J 10 8 5 4
|  K Q 9 7 K Q 9 7
| |
 K Q J 4 K Q J 4
|  A 10 3 A 10 3
| |
 | Q J 6 5 4 | |
 | A Q J 2 | |
 | 6 3 | |
 | 9 2 |
Here, North-South can take 11 tricks, while East-West take 9 tricks. 19
trumps, but 20 tricks. According to Cohen, this is attributed to the "purity"
factor.
It isn't, in fact. There is no magic in bridge, only logic. Tricks come from
combination of distribution and honors, nothing else. In this example, too.
What about North-South ? They have 21 HCP, but since ♥K is onside, the ♥J is just as good as ♥K, and the acting "King" will provide a useful discard, so they have 23 WP. Their SST is 4, which suggests 10 tricks, but there are 11, in fact. That extra trick comes from the fact that North-South have doubletons in the three side suits, and all of them are useful. Therefore, we adjust the SST to 3. We discussed this topic in more detail in I Fought The Law of Total Tricks.
East-West also have an SST of 3, but only 16 of their HCP are working. That is equivalent to 9 tricks.
 | A K 10 9 3 | |
 | 8 5 | |
 | A 2 | |
 | 8 7 6 5 | |
 8 7 8 7
| 
|  2 2
|
 K 7 K 7
|  10 9 6 4 3 10 9 6 4 3
| |
 J 10 8 5 4 J 10 8 5 4
|  K Q 9 7 K Q 9 7
| |
 K Q J 4 K Q J 4
|  A 10 3 A 10 3
| |
 | Q J 6 5 4 | |
 | A Q J 2 | |
 | 6 3 | |
 | 9 2 |
At the same time, North-South lose 5 WP. In the first case, South's ♥QJ were just as good as ♥KQ, but now they are no better than deuces. With 18 WP and an adjusted SST of 3, it's easy to understand why they now take two tricks fewer than when they had another 5 WP.
| |||||||||||||||||||||||||
|
This deal is published in Following The Law (page 72 à 52).
Cohen writes:
" Notice that there were 19 trumps and 20 tricks. The extra trick comes from the
extreme purity of the deal — no wastage in any suit."
But that explanation is wrong.
Truth about the deal is this:
North-South have 16 WP and 3 SST,
which is equivalent to 9 tricks. East-West have 24 WP and 3 SST,
quivalent to 11 tricks. It's all in the cards: distribution and useful honors.
Now let's swap two cards between the partners (♥8 and ♣4 between East and West, ♥3 and ♣2 between North and South). Then we get:
 | J 9 4 3 | |
 | A Q 6 3 | |
 | 10 8 | |
 | 10 8 3 | |
 A A
| 
|  10 2 10 2
|
 8 7 2 8 7 2
|  10 9 4 10 9 4
| |
 A K Q 7 4 3 A K Q 7 4 3
|  J 6 2 J 6 2
| |
 K 9 5 K 9 5
|  A Q J 6 4 A Q J 6 4
| |
 | K Q 8 7 6 5 | |
 | K J 5 | |
 | 9 5 | |
 | 7 2 |
Now, the same 19 total trumps produce only 18 tricks, two less than before.
Does moving a few spot cards around mean disappearance of the "extreme purity" ?
Then, why ?
Or, is it the truth that talking about 'purity' is not talking about the
real reason for the loss of these two tricks...
This is how we explain it: The swapping does not affect the WP for any side, but the SST go up from 3 to 4 for both sides. Therefore, each side loses one trick.
Good fit versus misfit
Cohen's second adjustment factor "fit" has already been discussed, when we looked at Vernes' corrections. We have shown there why a double fit often produces extra tricks. It was not because the second fit was some sort of a "second trump suit"; it had to do with distribution. Go back and take a look, if you forgot what we wrote.
When Cohen says a misfit often produces fewer tricks, we agree with him. If you have a singleton opposite KQJ7xx, it is possible that those honors are useless in your contract, while they will take two tricks on defense. Then, the effect is that your side will take fewer tricks in your contract, because 6 of your HCP are not working.
Shortness in partner's suit
What will happen, in the presence of a shortness opposite nothing wasted ?
If you have a singleton in partner's suit, where he has five small or Ace fifth, for example,
your side has no wasted honors in that suit — and still there may be fewer
total tricks than the Law of Total Tricks suggests.
This happens when there take place adverse ruffs. For some reason, Cohen skips
this issue. But we won't. When you lead the singleton suit and get one, two or even
three ruffs with otherwise useless trumps, what happens is that some of the
opponents' WP in that suit lose their value.
If they have ♥KQx opposite ♥J10x,
and we start our defense with ♥A,
heart ruff and later score a
second heart ruff, what has happened is that the opponents' hearts weren't
better than ♥xxx opposite ♥xxx, and what looked like 6 WP in reality was 0 WP.
This is another reason why HCP can't automatically be translated to WP. If an
honor doesn't take a trick, it is worth nothing.
Shape is important
Cohen's third factor, shape, is perfect. Actually, it's the most important of them all. It's so important that it has made the Law of Total Tricks obsolete.
 | K Q J 2 | |
 | K Q 3 | |
 | 8 5 4 | |
 | 8 6 2 | |
 8 5 8 5
| 
|  6 4 3 6 4 3
|
 8 6 5 8 6 5
|  9 7 4 2 9 7 4 2
| |
 K Q 2 K Q 2
|  J 10 6 J 10 6
| |
 A J 10 4 3 A J 10 4 3
|  K Q 7 K Q 7
| |
 | A 10 9 7 | |
 | A J 10 | |
 | A 9 7 3 | |
 | 9 5 |
This is the very first example in To Bid or Not to Bid (page 10).
The deal looks "extremely pure" to us, and still there are no extra tricks (an
indication that 'purity' is something that is best forgotten).
Now we will do
two changes.
First, we swap two cards between East and West (♥5 and ♦J).
 | K Q J 2 | |
 | K Q 3 | |
 | 8 5 4 | |
 | 8 6 2 | |
 8 5 8 5
| 
|  6 4 3 6 4 3
|
 8 6 8 6
|  9 7 5 4 2 9 7 5 4 2
| |
 K Q J 2 K Q J 2
|  10 6 10 6
| |
 A J 10 4 3 A J 10 4 3
|  K Q 7 K Q 7
| |
 | A 10 9 7 | |
 | A J 10 | |
 | A 9 7 3 | |
 | 9 5 |
If you had shown this deal to a Law guru and he had responded that the extra
trick comes from something called 'purity', you might even have believed in him. Now
you know better. The extra trick comes from East-West's improved distribution,
nothing else. In the first example, East-West had 16 WP and an SST of 5. Here,
they have 16 WP and an SST of 4.
Can anybody be surprised that the difference is
one trick ? Since the swap didn't affect North-South, they still take 9 tricks
with their 23 WP and an SST of 5.
From the original example, we now swap two cards between North and South (♠2 and ♣5).
 | K Q J | |
 | K Q 3 | |
 | 8 5 4 | |
 | 8 6 5 2 | |
 8 5 8 5
| 
|  6 4 3 6 4 3
|
 8 6 5 8 6 5
|  9 7 4 2 9 7 4 2
| |
 K Q 2 K Q 2
|  J 10 6 J 10 6
| |
 A J 10 4 3 A J 10 4 3
|  K Q 7 K Q 7
| |
 | A 10 9 7 2 | |
 | A J 10 | |
 | A 9 7 3 | |
 | 9 |
Now, North-South take 10 tricks, while East-West take 7 tricks as before. The difference is distributional again. The SST for North-South has been improved from 5 to 4, and the result is one trick for them. Note that the swap didn't do East-West any harm; they still take 7 tricks.
Both these swaps show that one of the bases for the Law of Total Tricks, namely the claim that "Bad breaks for one side translate into good breaks for the other. The Total Trick count is constant. (To Bid or Not to Bid, page 19)" is false. It may be that changes work both ways, but often they affect the tricks only for one side.
The small changes are the important ones
An interesting fact is that small changes are usually the ones affecting only one side: going from 3-3 to 4-2, or from 2-2 to 3-1 will reduce our SST, but it will often have no bad effect on the opponents. But bigger changes, like going from 3-3 to 5-1 will quite often have an effect on defense as well as on offense.
saved from url=http://www.newbridgelaw.com/